
Hassasiyet ve tekrarlanabilirlik özelliklerinin belirlenebileceği yöntemler sunan çok sayıda konumlandırma standardı mevcuttur. Kullanılan standarda bağlı olarak, aynı işleme merkezinde farklı hassasiyet ve tekrarlanabilirlik değerleri elde edilecektir. Çeşitli standart ve yönergeler kullanılması, satın alma işlemi sırasında farklı işleme merkezi birbiriyle kıyaslanmasını zorlaştırmaktadır. Standartları karşılaştırmadan önce bazı önemli kavramların tanımlanması gerekmektedir.
Hassasiyet. İdeal olarak, bir işleme merkezi her çalıştırıldığında, tam olarak önceden belirlenen konumda bulunacaktır. Her standart, hassasiyetin nasıl ölçüleceğini tanımlar. İşleme merkezi üreticileri için üç tip hassasiyet söz konusudur: tek yönlü ileri, tek yönlü geri ve çift yönlü. Bu durum; tıpkı atış yarışmasında ilk olarak hedefe doğru ilerleyerek ve daha sonra hedeften uzaklaşarak atış yapmak zorunda olan bir yarışmacıya benzetilebilir. Hedefe doğru ilerlerken yapılan atışların hassasiyeti tek yönlü ileri hassasiyet ve hedeften uzaklaşırken yapılan atışların hassasiyeti ise tek yönlü geri hassasiyettir. Genel hassasiyet düzeyi hesaplanırken tüm atışların aritmetik ortalaması dikkate alınır ve bu değer, her iki yönde yapılan atışların hassasiyet düzeyi dikkate alındığından, çift yönlü hassasiyet olarak adlandırılır.
Tekrarlanabilirlik. Şekil 12’de, bir atış yarışmasında kullanılan dört hedef gösterilmektedir. İlkinde (a), her bir atış arasındaki mesafe tekrarlanabilirliği ifade eder. Atışların tümü hedefin orta noktasına isabet etmesine rağmen, delikler bir desen oluşturduğu için atışı yapan kişinin dengesinin çok hafif bir şekilde bozulduğu söylenebilir. Mermiler, bir desen oluşturmak yerine tek bir delik üzerinde aynı noktaya isabet etseydi, tekrarlanabilirliğin mükemmel seviyede olduğu söylenebilirdi. Ancak, hedef üzerinde desen oluşması yine de tekrarlanabilirliği ifade eder. “a” hedefindeki delikler gibi, işleme merkezi oluşan kaymalar da hedef noktası etrafında görülür. “b” hedefinde de, tekrarlanabilirliğin oldukça iyi seviyede olduğunu gösteren, aralıkları dar bir desen görülmektedir. Dolayısıyla, atışı yapan kişinin her atışta sola doğru yatmış olduğu veya tüfek nişangahının hafifçe sola kaymış olduğu ve bunun da hassasiyet düzeyini düşürdüğü söylenebilir (hiçbir atış, hedefin orta noktasına isabet etmemiştir). “c” hedefi üzerindeki atışlar, atışı yapan kişi hedefe doğru ilerlerken ve “d” hedefi üzerindeki atışlar ise, atışı yapan kişi hedeften geriye doğru hareket ederken yapılmıştır. Dolayısıyla “c” hedefi ileri yönlü tekrarlanabilirlik seviyesini, “d” hedefi ise geri yönlü tekrarlanabilirlik seviyesini ifade eder.
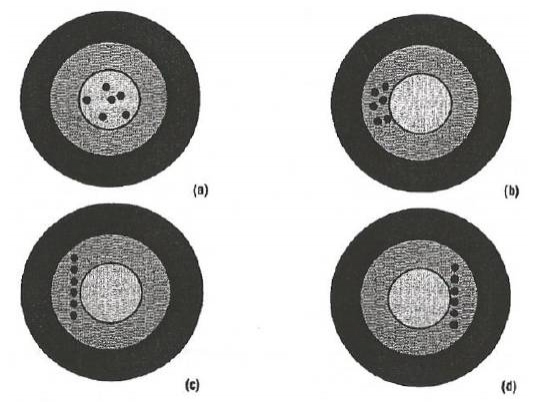
Şekil 12. Tekrarlanabilirlik örnekleri
Tekrarlanabilirlik, isabet noktaları arasındaki toplam mesafe üzerinden test edilir; “c” hedefi üzerinde en altta ve en üstte yer alan mermi delikleri arasındaki mesafenin 0.5 inç olduğu kabul edilirse, bu mesafenin tekrarlanabilirlik seviyesini ifade ettiği söylenebilir. Ayrıca burada, “c” ve “d” hedeflerinin bir arada göz önünde bulundurulduğu çift yönlü tekrarlanabilirlik de söz konusudur; yani “c” hedefi üzerinde en altta yer alan mermi deliğinin, “d” hedefi üzerinde en üstte yer alan mermi deliğine olan uzaklığı çift yönlü tekrarlanabilirlik değerini verir.
İşleme merkezine ilişkin tekrarlanabilirlik; ileri yönlü tekrarlanabilirlik, geri yönlü tekrarlanabilirlik, çift yönlü tekrarlanabilirlik ve dağılma olarak tanımlanabilir ve herbiri farklı şekilde hesaplanır.
Kayıp Hareket. Kayıp hareket hareketin başlatıldığı; ancak kayıp hareket giderilene kadar (tıpkı makaradaki halatın boşluğunun alınarak gerdirilmesi gibi) hiçbir çalışma gerçekleştirilememesi anlamına gelir. “c” ve “d” hedeflerine ateş eden nişancıda da kayıp hareket görülmektedir. “c” hedefinde tüm delikler merkezin solundayken, “d” hedefinde tüm delikler merkezin sağındadır. Bunların arasındaki fark kayıp harekettir. Kayıp hareket ile ilgili diğer ifadeler geri dönüş hatası veya ortalama geri dönüş hatasıdır.
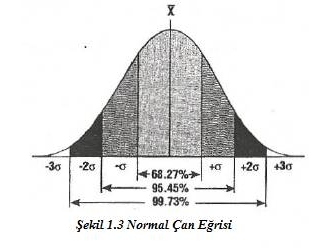
Veri Toplama. Bir işleme merkezinde; altı bölgesel hedef ve “sıfır” olarak kabul edilen, rasgele seçilmiş herhangi bir başlangıç noktasına göre belirlenen konumların bulunduğunu varsayalım. Eğer işleme merkezinde bu altı hedefin tümüne göre konumlanır, ters yönde hareket eder ve aynı altı hedefe göre sıfır noktasına tekrar konumlanırsa ve tüm duruşların hata ölçümü yapılırsa (durma noktasından hedefe olan uzaklık), hedef üzerinden gerçekleştirilen her hareket sonucunda on iki adet veri referansı elde edilir. İşlem sekiz defa tekrarlanırsa, 84 adet veri referansı toplanır. Bu verilerden ( her biri “örneklem” ve tamamı “evren” veya “populasyon” olarak adlandırılır) yola çıkarak; hassasiyet, tekrarlanabilirlik ve kayıp hareket özellikleri, normal eğri hesaplamaları kullanılarak belirlenebilir. Bunu yaparken ilk adım, tümünü toplamak ve 84’e bölmek suretiyle 84 örneklemin ortalamasını (aritmetik ortalama) hesaplamaktır. Bulunan ortalama çan şekilli eğrinin orta noktasıdır ve “x” sembolü ile gösterilir. Daha sonra, orta noktaya olan ortalama uzaklığı ifade eden standart sapmayı (sigma veya ϭ) bulunuz. Normal çan eğrisinin gösterildiği Şekil 13’te de görülebileceği gibi; bir standart sapma (bir- ϭ) eğri alanının %68.27’sini, iki ϭ uzaklığı eğrinin %95’ini ve üç ϭ uzaklığı ise eğrinin %99.73’ünü kaplar. Temelde, bu durum örneklemlerin %68.27’sinin bir ϭ standart sapma alanı (artı ve eksi) ve tüm örneklemlerin %99.73’ünün üç (artı ve eksi) standart sapma alanı içinde yer alması gerektiğini gösterir. Aşağıdaki formül, küçük ölçekli bir örneklemin (örn. 84) standart sapmasını bulmak için kullanılır.

Burada;
∑, “toplamı”
X, bireysel ölçümü
x, ortalama değeri
n ise toplam ölçüm sayısını ifade eder. Geniş bir örneklemde ise, (n-1) yerine n değerine bölünüz.
Standartların Yorumlanması. JIS B 6336 standardı hariç olmak üzere aşağıda kısaca ele alınan standartların her biri, birçok üreticinin kullanılan standarttan bağımsız olarak yaklaşık değerler belirtmesine rağmen, sağlanan değerlere ilişkin toplam değerleri ortaya koymaktadır. Bu durum, daha düşük bir değerin oluşacak olması şeklinde yorumlanabilir. İstatistiksel olarak çift yönlü verileri kullanarak hesaplama yapan tek standart NMTBA’dır. Diğer istatistiksel standartlar kendi çift yönlü verilerini, bağımsız ileri ve geri yönlü verileri kullanarak oluştururlar. Bu yöntem, daha iyi veya daha kötü olarak değerlendirilmez; ancak NMTBA standardında görülen sapmaların daha küçük olması, bu standartla elde edilen değerlerin daha başarılı olduğu yönünde bir izlenim yaratmaktadır. Aslında NMTBA en zorlayıcı standarttır. Özetle, aşağıda tanımlanan standartların tamamı işleme merkezlerinin doğrusal konumlanmasını analiz etmek için kullanılabilir. Ancak; kullanılan herhangi bir standart, diğer standartlara kıyasla işleme merkezi hassasiyetinin daha yüksek olduğunu gösterebilir.
Aynı işleme merkezi uygulanan testlere dayalı olarak, altı standardın tümü için elde edilen verilerin karşılaştırması Tablo 6’da gösterilmiştir. Veriler inç ölçü sisteminde olup, tüm ölçümler µin (mikroinç veya inçin milyonda biri) cinsinden belirtilmiştir.
NMTBA (ABD), son yıllarda Amerikan işleme merkezlerinde hakim şekilde kullanılan standarttır ve bu araştırmada diğer standartlar için bir tür karşılaştırma standardı olarak kabul edilecektir.
ISO 230-2-1988 (Avrupa) standardı; ileri, geri ve çift yönlü tekrarlanabilirliği hesaplar. Bu standartla hesaplanan çift yönlü değerler NMTBA’dan farklıdır; çünkü NMTBA standardı çift yönlü tekrarlanabilirliği istatistiksel olarak hesaplarken; ISO standardı, ileri ve geri altı-sapma alanı (ϭ) ile en geniş sapma alanını veya bir başka ifadeyle üç ileri sapma alanı (ϭ), üç geri sapma alanı (ϭ) ve mutlak kayıp hareket değerinin toplamını kullanmaktadır. Ayrıca ISO, en yüksek kayıp hareket değerine sahip nokta (NMTBA) yerine, kayıp harekete ilişkin ortalama hata değerini kullanır. Bu da NMTBA standardında elde edilen değerlerin yaklaşık %40’ına denk gelmektedir. ISO standardında hassasiyet değeri, x + 3ϭ ileri ve geri sapma alanı verilerinde işaretli en büyük sayı tespit edilerek ve ileri ve geri x + 3ϭ verilerinden, işaretli en küçük sayı çıkarılarak hesaplanır. NMTBA; ileri yönlü, geri yönlü ve çift yönlü tekrarlanabilirlik değerlerini istatistiksel olarak hesaplar. ISO, yalnızca ileri yönlü ve geri yönlü verileri kullanır.
BSI BS 4656 Part 16 (Büyük Britanya) standardı, içerdiği “ortalama çift yönlü konum sapması” (D) olarak adlandırılan kavram haricinde ISO standardı ile bire bir aynıdır. D değeri, ileri ve geri örneklem ortalamalarının en büyüğü, ileri + geri örneklem ortalamalarının en küçüğüdür. D değerinin, NMTBA standardı kapsamında bir eşdeğeri yoktur.
VDI/DGQ 3441 (Almanya) standardı, ileri ve geri hassasiyet değerleri ile ileri ve geri tekrarlanabilirlik değerlerini, NMTBA standardında görülen şekilde belirlemektedir. Konumlandırma belirsizliği (P), çift yönlü hassasiyet ile ilişkilidir; ancak bu değer, ortalamalar ve ortalamaların ortalamaları kullanılarak hesaplanır. Tablo 6’da gösterilen örnekte olduğu gibi, bu prosedür gerçek sayıları NMTBA değerine kıyasla %40 azaltır (1966’ya karşı 851). Konumsal sapma (Pa), ortalamalar arası hassasiyet olarak ifade edilir; bir başka ifadeyle ileri hareket ortalamaları arasındaki fark ile geriye hareket ortalamaları arasındaki farkın ortalamasıdır. Aynı şekilde, bu sonuçlar da oldukça küçük sayıdadır ve NMTBA değerleri ile herhangi bir bağdaşıklık göstermez. Konumsal dağılma (Ps), çift yönlü tekrarlanabilirlik ile ilişkilidir. VDI standardı, ileri ve geri örneklemlerden ϭ sapma alanı ortalamasını dikkate alır, mutlak değeri hesaplar ve ilgili değeri altı ile çarparak en yüksek değeri kullanır. NMTBA standardı, ϭ sapma alanını istatistiki olarak hesaplar; bu değeri üç ile çarpar ve bu 3 ϭ değerini çift yönlü tekrarlanabilirlik düzeyi olarak kullanır. Geri hareket hatasının (U), NMTBA standardındaki “kayıp hareket” ile bağdaştığını ve bunların aynı değere sahip oldukları söylenebilir. VDI/DGQ 3441’in bir standart değil, yalnızca bir yönerge olduğu unutulmamalıdır.
JIS B 6336-1986 (Japonya) standardı, hassasiyet ve tekrarlanabilirliği diğer çoğu standarttan farklı değerlendirir. Hassasiyet, her yönde bir kez olmak kaydıyla, kızağın neredeyse tüm hareketini kapsayan eşit artışlara göre konumlanma ile ölçülür. Hassasiyet değeri, artı veya eksi yöndeki en büyük hata aralığıdır. Tekrarlanabilirlik için, yedi turun sona erdiği noktaya göre konumlanma gerekir. İşlem hareketin ortasında ve tam tersi yönde tekrarlanır. Üç noktanın herhangi birindeki en büyük hata değeri kaydedilir. Daha sonra işlem tam tersi yönde tekrarlanır ve her iki yöndeki en büyük hata değeri, ± bir değer vermek için ikiye bölünür. Kayıp hareket, bilinen bir artışla aynı yönde devam ederken aynı artışla ters yöne hareket ederek ve herhangi bir referans noktasına göre konumlanarak hesaplanır. İşlem hareketin her iki uç noktasında ve merkezinde tekrarlanır. Her konumda veriler yedi kez toplanır, bu verilerin ortalaması alınır; üç ortalamanın en büyüğü kayıp hareket olarak ifade edilir.
Tablo 6. Konumlandırma Standartları ile ilgili Sayısal Karşılaştırmalar
| Standart | NMTBA | ISO | VDI | BSI | JIS | B5.54 |
| Hassasiyet | ||||||
| İleri Hassasiyet | 982 | NA | 982 | NA | NA | NA |
| Geri Hassasiyet | 1030 | NA | 1030 | NA | NA | NA |
| Çift-Yönlü Hassasiyet | 1966 | NA | NA | NA | NA | NA |
| Hassasiyet | NA | A 1109 | NA | A 1109 | NA | A 937 |
| Konumsal Sapma | NA | NA | Pa 449 | NA | NA | NA |
| Konumsal Belirsizlik | NA | NA | P 851 | NA | NA | NA |
| Ortalama Konumsal Sapma | NA | NA | NA | D 799 | NA | NA |
| İleri Yönlü Kesin Doğruluk | NA | NA | NA | NA | 600 | NA |
| Geri Yönlü Kesin Doğruluk | NA | NA | NA | NA | 480 | NA |
| Çift-Yönlü Kesin Doğruluk | NA | NA | NA | NA | NA | NA |
| Tekrarlanabilirlik | ||||||
| İleri Yönlü Tekrarlanabilirlik | 182 | R↑182 | 182 | RU+182 | NA | NA |
| Geri Yönlü Tekrarlanabilirlik | 280 | R↓280 | 280 | RU-280 | NA | NA |
| Çift-Yönlü Tekrarlanabilirlik | 1966 | R | NA | RB 820 | NA | NA |
| Konumsal Dağılma | NA | NA | Ps 222 | NA | NA | NA |
| İleri Yönlü Kesin Tekrarlanabilirlik | NA | NA | NA | NA | 420 | NA |
| Geri Yönlü Kesin Tekrarlanabilirlik | NA | NA | NA | NA | NA | NA |
| Çift-Yönlü Kesin Tekrarlanabilirlik | NA | NA | NA | NA | NA | NA |
| Kayıp Hareket | ||||||
| Kayıp Hareket | 629 | N/A | N/A | N/A | 180 | N/A |
| Ortalama Geri Dönüş Hatası | N/A | B 203 | N/A | B 203 | N/A | N/A |
| Geri Dönüş Hatası | N/A | N/A | U 629 | N/A | N/A | R?629 |
ASME B5.54-92 (ABD), ortalama saplamalara göre hassasiyet düzeyini belirler. İleri veya geri yönlü olup olmamasına bakılmaksızın, ileri yönlü x aritmetik ortalamadan en büyük ve en küçük değerler kullanılır. Standart, üç etaplı hareketleri belirler. Tablo 6’nın oluşturulması için kullanılan veriler yedi etaplı hareketlerden elde edildiğinden, Tablo’daki rakamlar normalden daha geniş bir aralığı yansıtmaktadır. Ortalamalardan, ek bir doğrusal performans değeri de elde edilebilir. Pek çok istatistiksek standart için ortak bir kriter olan bu rakam “maksimum geri dönüş hatası” (Rmax) olarak ifade edilir ve ileri ve geri yönlü aritmetik ortalama x arasındaki maksimum fark şeklinde tanımlanır. ASME B5.54-92 standardı, JIS 6336 standardı ile benzer şekilde ölçülebilen çift yönlü tekrarlanabilirlik değerini hesaplar. Ancak, çoğu imalatçı ve lazer yazılımları tekrarlanabilirliği direkt olarak hedef noktalara daha fazla veri gönderilmesini sağlayan hassasiyet döngülerinden hesaplamaktadır (standart olarak gerekli iki lokasyonda gerçekleştirilen on adet çift yönlü vuruş ile karşılaştırıldığında); standardın bu bölümü ile ilgili değişiklik yapılmasına yönelik talep değerlendirme aşamasındadır.






